Savez vous comment calculer l aire d un cercle ?
Dans cet article, vous allez découvrir quelle formule utiliser pour :
- Calculer l’aire d un cercle avec son rayon, son diamètre ou son périmètre.
- Déterminer l aire d’un demi cercle ou d’un quart de cercle.
- Calculer la surface d’un cercle à partir de la surface de l’un de ses secteurs.
En bref, à la fin de ce cours, les cercles n’auront plus de secret pour vous !
Si vous voulez lire d’autres leçons et faire de nouveaux exercices gratuitement, alors n’hésitez pas à consulter notre rubrique consacrée au Soutien Scolaire.
Comment calculer l aire d un cercle ?
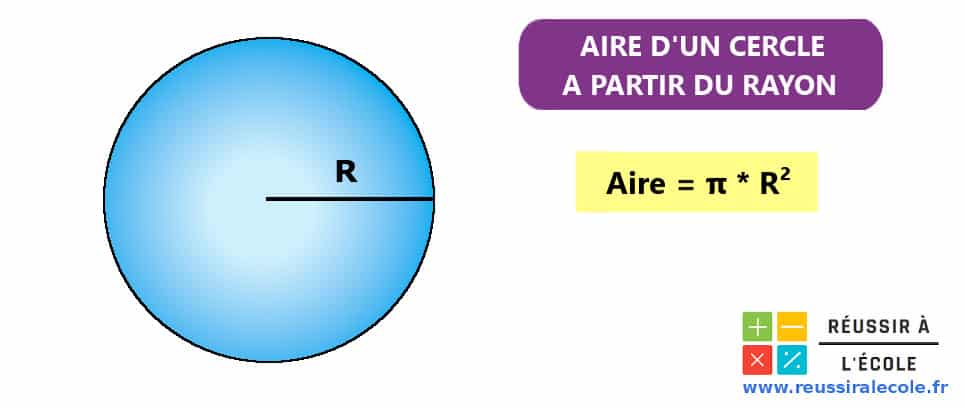
On calcule l’aire d un cercle (d’un disque) de rayon R grâce à la formule suivante :
Dans cette formule, R désigne le rayon. Il correspond donc à la longueur entre le centre et son bord.
π (Pi) est une constante mathématique dont la valeur approximative est environ égale à 3,14.
Pour calculer l’aire d un cercle, nous vous conseillons donc de procéder de la façon suivante :
- Repérez ou déterminer R, la valeur du rayon.
- Mettez le rayon R au carré et multipliez par PI ou π.
- Indiquez le résultat obtenu en utilisant l’unité métrique mise au carré.
Par exemple, si le rayon est mesuré en mètre, alors la surface du disque sera en mètre carré.
Calcul de la surface d un cercle à partir du diamètre
On peut calculer l’aire d un cercle (disque) à partir de son diamètre. En effet, par définition le diamètre est un segment de droite, qui traverse un cercle en son centre et qui le coupe en deux points à égale distance du centre.
Ainsi on peut dire que le diamètre est toujours égal au double du rayon.
A partir de cette information, on peut écrire que :
D = 2 x R, donc R=D/2
Cette égalité nous permet de transformer la formule de la surface d’un disque de la façon suivante :
Comment calculer l aire d un cercle avec la circonférence ?
Lorsqu’on connaît le périmètre d’un cercle, sans en connaître le rayon ou le diamètre, on peut facilement calculer la surface du disque.
En effet, on sait que :
- Le périmètre d’un cercle est égal à :
- La surface d’un disque est égal à :
On peut donc écrire les équivalences suivantes :
Ainsi on conclut que la surface d’un disque est aussi égale au carré de son périmètre divisé par quatre fois la valeur de Pi.
Comment trouver la surface d un secteur de cercle ?
Dans certains exercices de géométrie, il arrive qu’on nous demande de calculer la surface d’un secteur de disque.
Alors comment faire ?
Tout d’abord, on sait que sa surface entière est égale à Pi multiplié par le rayon mis au carré. Mais cette égalité est valable pour un angle total de 360°.
Ainsi pour un secteur dont l’angle est égale à une valeur notée C, on peut dire que :
Trouver la surface d un disque à partir d’un secteur
Parfois, il arrive qu’on connaisse la surface d’un secteur dont l’angle vaut C.
Et, il faut alors déterminer la surface du disque dans sa totalité.
Pour cela, voici une formule bien pratique à utiliser :
D’ailleurs, nous souhaitons vous rappeler qu’il est possible de déterminer facilement l’angle d’un secteur à l’aide d’un rapporteur.
Pour cela, il faut suivre la méthode suivante :
- Tout d’abord, on aligne la base du rapporteur le long de l’un des 2 rayons.
- Ensuite, on ajuste le point central du rapporteur sur le centre du cercle.
- Puis on lit la mesure de l’angle correspondant à la position du deuxième rayon formant le secteur.
Comment calculer l aire d un demi cercle ?
Comme nous l’avons vu, l’aire d un disque est égale à :
On en déduit alors que l’aire d un demi cercle ou d’un demi-disque est égale à la moitié de celle d’un disque entier.
On peut donc écrire que :
D’ailleurs, si on utilise la formule vu précédemment sur la surface d’un secteur, alors on peut écrire que l’aire d un demi cercle vaut :
Comment calculer la surface d un quart de cercle ?
Par analogie avec le chapitre précédent, on peut dire que l’aire d un quart de cercle est égale à l’aire d un disque divisée par 4.
On obtient donc la formule suivante :
Quelle est la définition d’un cercle ?
Un cercle O de centre A et de rayon R se définit par l’ensemble des points se trouvant à la distance R du point A. Alors la distance entre les points du contour et le centre A est appelée le rayon R. On définit donc ce type de figure géométrique grâce à leur centre et à leur rayon.
Quelle est la définition d’un disque ?
On appelle un disque O de centre A et de rayon R, l’ensemble des points qui forment le cercle ainsi que ceux qui se trouvent à l’intérieur.